
A-Netze - Modellieren mit Perspektiven
Fährmannbeispiel
(das Applet erscheint gleich als separates Fenster.)
Es wird dabei das bekannte Denkspiel von Fährmann, Wolf, Ziege und Kohlkopf modelliert:
Ein Fährmann steht vor folgendem Problem: Er muß einen
Fluss in einem kleinen Boot überqueren, und muß einen Wolf, eine
Ziege und einen Kohlkopf mit zum anderen Ufer nehmen.
Das Boot ist leider so klein, dass außer ihm nur ein Tier oder der
Kohlkopf mit ins Boot passen. Allerdings muss er auch auf die Tiere und den
Kohlkopf aufpassen, denn ist der Wolf mit der Ziege allein, so frisst der
Wolf die Ziege, ebenso frisst die Ziege den Kohlkopf, wenn sie mit ihm allein
ist (somit darf z.B. der Fährmann nicht den Wolf zuerst mitnehmen, sonst
ist der Kohlkopf zum Fressen freigegeben
1. Perspektive - Fähigkeiten
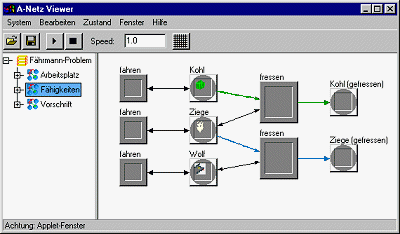
Die Regeln des Spiels, die die Passagiere betreffen werden modelliert. "fahren"
können die Passagiere einzeln, fressen betrifft jeweils zwei
Passagiere.
Würde man für "fahren" eine einzige Transition mit Kanten zu den
drei möglichen Passagieren eintragen, würde man damit verlangen,
dass die Passagiere gemeinsam "fahren".
Wenn ein Passagier gefressen ist, kann er nicht mehr fahren.
Beim Fressen ist durch Kantenlabel festgelegt, wer die Rolle des Opfers
bekommt.
(Das Kantenlabel ist im Kontextmenü der Kanten einzusehen und zu
ändern.)
Zur Deutlichkeit sind hier die Kanten mit gleichem Label farbig hervorgehoben.
2. Perspektive Arbeitsplatz
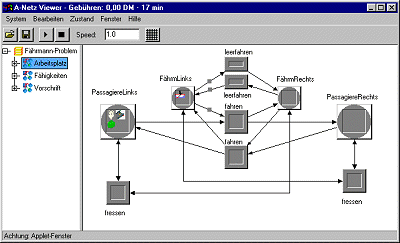
Statt dies in die erste Perspektive zu integrieren, wird eine neue Perspektive gewählt, die auf diese Sicht spezialisiert ist.
"fahren" hat je zwei Eingangs- und Ausgangskanten und gibt damit die Spielregel wieder, dass der Fährmann höchstens einen Passagier mitnehmen kann, der dann am anderen Ufer erscheint.
"fressen" kann am linken oder am rechten Ufer geschehen, aber nur, wenn der Fährmann am anderen Ufer ist. ("fressen" hat je 3 Doppelkanten, die 2 Doppelkanten der Passagiere liegen übereinander.)
Weil die Token (Aspekte) beider Perspektiven jedoch als "siblinks"
miteinander verbunden sind und die Schaltregeln für A-Netze in diesem
Fall verlangen, dass Transitionen mit gleichem Label, die in beiden Perspektiven
vorkommen, nur synchron schalten können, sind nicht alle Schaltfolgen
mehr möglich.
Weil ein gefressener Passagier in der Fähigkeiten-Perspektive nicht
mehr fahren kann, wird er auch in der Arbeitsplatzperspektive nicht mehr
mitgenommen. (Konsequenterweise sollte man ihn dann löschen. Darauf
wurde hier verzichtet. - Es ist eine gute Übungsaufgabe für
später.)
Außerdem verbietet die Fähigkeitenperspektive das "fressen" von
Kohl und Wolf auch in der Arbeitsplatzperspektive.
Mit diesen beiden Perspektiven sind die Spielregeln vollständig modelliert, es sind alle Schaltfolgen möglich - auch die ungünstigen, die auch ein menschlicher Spieler machen dürfte.
2. Perspektive (Dienst-) Vorschrift
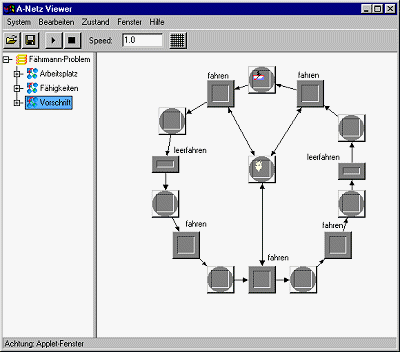
Wie man schnell sieht, kommt es nur auf die Position der Ziege an, weil sie für beide "fressen"-Regeln kritisch ist.
Wegen der A-Netz-Schaltregeln (s. o.) verlangt eine Transition "fahren" mit
Doppelkante zur Ziege, dass die Ziege mitgenommen wird, während eine
Transition "fahren" ohne Kanten zur Ziege verbietet, dass die Ziege mitgenommen
wird (sie müsste ja in allen Perspektiven am Schaltvorgang mit dem Label
"fahren" beteiligt sein.)
Die anderen Passagiere werden hier nicht erwähnt, so dass nicht festgelegt
wird, ob hier bei den "fahren"-Transitionen ohne Ziege der Wolf oder der
Kohl mitgenommen wird. Beides kommt vor und steht für verschiedene
Lösungen des Spiels.
Nach einem Umlauf des Fährmanns in diesem Teilnetz, sind alle Passagiere nach rechts übergesetzt, und im nächsten Umlauf bringt der Fährmann sie wieder zurück.
Das Verhalten von getrennt stehenden Perspektiven kann beobachtet werden, wenn vor dem ersten Start die siblink-Aspekte in den anderen Perspektiven gelöscht werden. Z. B. wird die Vorschrift nicht mehr beachtet, wenn man vor dem Start den Fährmann in der Vorschriftsperspektive löscht.
A-Nets are free